What is the Birthday Paradox?
The birthday paradox is the surprising mathematical result that in a room of just 23 people, there’s a greater than 50% chance that two of them share the same birthday. Counter-intuitive but true! I remember a teacher demonstrating this in school and being very impressed. I’m not going to dive deep into the proof here, because you can read lots more detail in many other places. Instead, I’ll focus on how this concept applies to Ethereum.
The birthday paradox has a general formula. In a domain with N possible values, a 50% chance of collision occurs when you’ve made approximately R selections:
R = 1.177 * SQRT(N)
For the birthday situation, where N = 365 (we ignore leap years!), the formula comes out to R = 22.486. This means 23 people takes us over the 50% mark. We can apply this formula to common Ethereum identifiers to get a feel for how unique they really are.
Applying the Birthday Paradox to Ethereum Identifier Spaces
Function Selectors
A function selector is made up of 4 bytes, which is 32 bits, and so the selector values live in 2^32 space. This means there are around 4.2 billion possible values, which kind of sounds a lot. But if we apply the birthday formula, we get R = 77,136 which isn’t a lot. We’d only need 77 thousand different functions to have a decent chance of finding two with the same selector.
There are examples of this in the wild. These examples are a bit skewed because it is pretty easy to brute-force such a small identifier space to manufacture collisions. We can use 4byte.directory to view (at the time of writing) a 6-way collision for 0xa9059cbb:
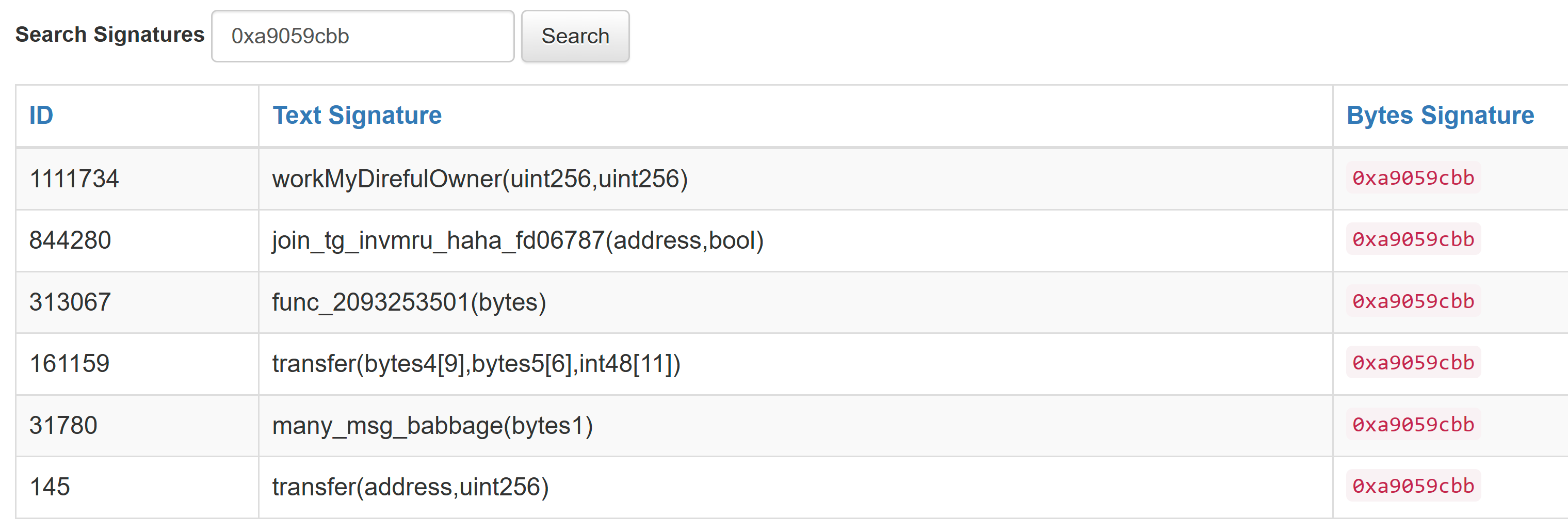
We can see that the above list contains function names that don’t look like they are “naturally occuring”. Some of the function names contain what looks like salt or nonce values at the end, so were likely brute-forced. However, the point still stands that the function selector identifier space is relatively small, and natural collisions will happen.
Ethereum Private Keys
This is an interesting one. An Ethereum address, as we know, is 20 bytes long, but the private key is 32 bytes long. So many (many, many) private keys map to the same address. When we’re applying the birthday formula here, we need to apply it to the 20-byte address space, because that’s where the collisions are important.
So 20 bytes is 160 bits and we’re in a much larger space now. The 2^160 space contains 1.4 * 10^48 possible values. This is a very large number.
We apply the birthday formula to get R = 1.4 * 10^24. This is still a very large number. For comparison, the number of grains of sand on earth is 1 * 10^21, depending on who counts it. We’re still an easy thousand times larger than that. When dealing with such large numbers, we can quickly approximate the birthday formula by halving the power of 2 exponent, so a 2^160 space needs 2^80 selections for a 50% chance of collision.
Whilst 10^24 (which we can write also as 2^80) is a large number, there is a lot of compute power around these days. A recent bug bounty paid out for an address collision bug where the compute power required was based on comparisons with the compute power of the bitcoin network. The point is that, with sufficient resources, it would be feasible today to produce a 160-bit address collision. Remember, though, that this is a collision for a random address. It is definitely not a “here is a specific address give me the private key” situation.



